È passato un po’ di tempo dall’ultimo articolo che ho scritto. In un certo senso potremmo anche dire che era ora di scrivere qualcosa di nuovo, d’altro canto non mi andava di scrivere qualcosa tanto per scrivere, senza un vero argomento. Tra le altre cose ho iniziato l’università, e una lezione di laboratorio di informatica mi ha dato l’ispirazione per questo articolo, che tratta del calcolo di pi greco.
Nel corso di informatica siamo partiti dai rudimenti del C, e presto siamo arrivati alle strutture decisionali e ai cicli. Uno degli esercizi della lezione di cui parlavo consisteva nello scrivere un programma che permettesse di calcolare un’approssimazione di pi greco tramite il metodo Monte Carlo. Un gran classico.

Per chi non lo conoscesse, vediamolo un attimo. Si consideri un quadrato di lato e un quadrante circolare di raggio
inscritto nel quadrato. Si immagini di disporre casualmente un numero di punti molto grande all’interno del quadrato. Grazie al numero molto grande e alla distribuzione casuale, possiamo approssimare la misura delle aree con il numero di punti contenuto in esse. Rappresentiamo il numero dei punti nel quadrato con
. Rappresentiamo il numero di punti nell’area del cerchio con
perché consideriamo solo un quadrante del cerchio di raggio
. Notiamo subito che:
Da cui:
Generati molti punti è possibile ricavare un’approssimazione del valore di pi greco dal rapporto dei punti nel cerchio su quelli nel quadrato, moltiplicato per quattro. È probabilmente il metodo più inefficiente per calcolare pi greco con un computer, ma secondo me è uno dei più interessanti.
Abbiamo detto che sono necessari tanti punti per fare questo calcolo, ma tanti quanti? Dal numero di punti dipende la precisione della nostra approssimazione di pi. Non so se ci sia una regola per determinare quanti a fronte di una certa approssimazione, ma possiamo fare delle prove.
Proviamo a fare 5 prove (per fare poi una media, fare una sola prova sarebbe poco indicativo) per ogni potenza di 10 da a
.

Vediamo che con centomila punti otteniamo già le prime due cifre decimali. Con un miliardo di punti possiamo ottenere una precisione alla quarta cifra decimale, ma il tempo di computazione inizia a diventare significativo, circa 55 secondi.
Questo è il codice in C usato, davvero semplice per chi mastica anche solo le basi di questo linguaggio:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define POINTS 1000000000
int main()
{
srand(time(NULL));
double x,y,pi;
unsigned long int app=0,j=0;
for(j;j<POINTS;j++)
{
x=rand()/(double)RAND_MAX;
y=rand()/(double)RAND_MAX;
if(x*x+y*y<=1)
{
app++;
}
}
pi=(4.0*app)/j;
printf("%lf\n", pi );
return 0;
}
Potremmo anche eseguire il programma con 10 milioni di punti, ma il tempo di calcolo decuplicherebbe, arrivando a una decina di minuti per una singola iterazione. Se volessimo eseguirlo cinque volte, per poter calcolare media e deviazione standard, dovremmo attendere quasi un’ora.
Controllando il consumo di risorse di sistema durante l’esecuzione del programma però notiamo una cosa: nel mio caso il programma occupa solo il 12,5% della potenza di calcolo disponibile! Il perché è presto detto: stiamo eseguendo il programma su una macchina quadcore, che è in grado di eseguire 8 thread contemporanei. Il programma è però composto da una serie lineare di istruzioni, che non possono essere divise in più thread. Viene quindi eseguito un solo thread, limitando la potenza di calcolo. D’altro canto la programmazione su più thread richiede competenze di informatica avanzate, rispetto alle mie.
Game over? No! È a questo punto che interviene la follia computazionale che ha dato il titolo a questo articolo. Se non so fare un programma multithread, posso imparare. O almeno imparare giusto il minimo necessario a eseguire questo programmino su più thread. E anche se il sito di Salvatore Aranzulla purtroppo non contiene un tutorial sulla programmazione multithread, non è difficile trovarne qualcuno in rete.
Ho fatto riferimento al tutorial di randu.org, e dopo una mezz’oretta di lettura e i consigli di qualche amico ero già in grado di scrivere un “Hello World” per ogni thread. Poco dopo avevo prodotto il mio primo programma multi-thread (frutto in larga parte di una magistrale opera di copia-incolla dal tutorial, ma non è un crimine):
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <pthread.h>
#define NUM_THREADS 8
#define THREAD_POINTS 1250000000
/* create thread argument struct for thr_func() */
typedef struct _thread_data_t {
int tid;
int app;
} thread_data_t;
/* thread function */
void *thr_func(void *arg) {
thread_data_t *data = (thread_data_t *)arg;
srand(time(NULL)*data->tid);
printf("Thread numero %d\n", data->tid);
double x,y;
int j=0;
data->app=0;
for(j;j<THREAD_POINTS;j++){
x=rand()/(double)RAND_MAX;
y=rand()/(double)RAND_MAX;
if(x*x+y*y<1){
data->app++;
}
}
pthread_exit(NULL);
}
int main(int argc, char **argv) {
pthread_t thr[NUM_THREADS];
int i, rc;
double pi=0;
clock_t begin = clock();
/* create a thread_data_t argument array */
thread_data_t thr_data[NUM_THREADS];
/* create threads */
for (i = 0; i < NUM_THREADS; ++i) {
thr_data[i].tid = i;
if ((rc = pthread_create(&thr[i], NULL, thr_func, &thr_data[i]))) {
fprintf(stderr, "error: pthread_create, rc: %d\n", rc);
return EXIT_FAILURE;
}
}
/* block until all threads complete (e stampa i punti nel cerchio per ogni thread concluso) */
for (i = 0; i < NUM_THREADS; ++i) {
pthread_join(thr[i], NULL);
printf("%u\n",thr_data[i].app);
}
clock_t end = clock();
printf("Tempo di computazione: %lf s\n", (double)(end - begin)/CLOCKS_PER_SEC);
return 0;
}
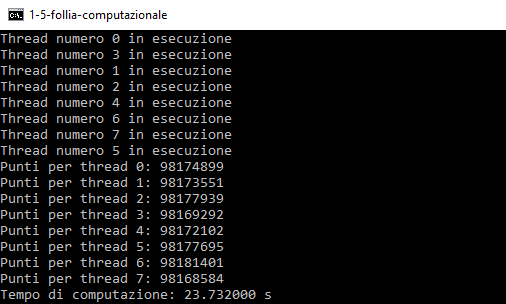
In questo modo il computer esegue 10 miliardi di punti in circa 3 minuti, sfruttando tutta la potenza di calcolo che ha a disposizione. Eseguendo il programma cinque volte si ottengono questi valori:
| 3,141522579 | 3,141519694 | 3,141521386 | 3,141523963 | 3,141525478 |
Che hanno una media di 3,14152262 e una deviazione standard di 0,0000022393. I valori sono molto coerenti tra loro, ma il valore è sbagliato! L’unica cosa che può andare male in questa funzione è la generazione dei numeri casuali, il resto è ciò che la matematica impone. Ad uno sguardo più approfondito la funzione rand() è molto limitata: nonostante garantisca una distribuzione equa dei numeri generati, è in grado di generare solo 32768 valori. Per i due assi X e Y può al massimo generare una griglia di 32768 x 32768 punti, ovvero poco più di un miliardo di punti. Anche se possono sembrare tanti, dobbiamo ricordare stiamo lavorando con un numero di punti simile, quindi poi così tanti non sono.
Bisognerebbe aumentare il numero di valori che la funzione rand() può generare. Potremmo ad esempio sommare due valori della rand(), ma i valori generati dalla somma non avrebbero più la distribuzione uniforme della funzione rand(). Guardando un po’ su google, si trova un topic su stackoverflow, in cui un utente suggerisce di usare la formula a*(RAND_MAX+1)+b in cui a e b sono due numeri casuali generati da rand(). Questa funzione dovrebbe generare numeri casuali equamente distribuiti, con massimo (RAND_MAX+1)^2-1. Ho fatto una veloce prova della distribuzione dei valori e mi è sembrata abbastanza uniforme, ma non posso garantirlo. In questo modo possiamo generare 1073807360 x 1073807360 punti, ovvero poco più di un trilione di punti. Saranno abbastanza per noi!
In ogni caso questo è il codice:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <pthread.h>
#define NUM_THREADS 8
#define THREAD_PI_ITERATIONS 1250000000
/* create thread argument struct for thr_func() */
typedef struct _thread_data_t {
int tid;
int app;
} thread_data_t;
/* thread function */
void *thr_func(void *arg) {
thread_data_t *data = (thread_data_t *)arg;
srand(time(NULL)*data->tid);
printf("Thread numero %d\n", data->tid);
double x,y,x1,x2,y1,y2,pi;
int j=0;
data->app=0;
for(j;j<THREAD_PI_ITERATIONS;j++){
x1=rand();
x2=rand();
y1=rand();
y2=rand();
x=x1*(RAND_MAX+1)+x2;
x=x/(((RAND_MAX+1.0)*(RAND_MAX+1.0))-1.0);
y=y1*(RAND_MAX+1)+y2;
y=y/(((RAND_MAX+1.0)*(RAND_MAX+1.0))-1.0);
if(x*x+y*y<1){
data->app++;
}
}
pthread_exit(NULL);
}
int main(int argc, char **argv) {
pthread_t thr[NUM_THREADS];
int i, rc;
double pi=0;
/* create a thread_data_t argument array */
thread_data_t thr_data[NUM_THREADS];
/* create threads */
for (i = 0; i < NUM_THREADS; ++i) {
thr_data[i].tid = i;
if ((rc = pthread_create(&thr[i], NULL, thr_func, &thr_data[i]))) {
fprintf(stderr, "error: pthread_create, rc: %d\n", rc);
return EXIT_FAILURE;
}
}
/* block until all threads complete (e stampa i punti nel cerchio per ogni thread concluso) */
for (i = 0; i < NUM_THREADS; ++i) {
pthread_join(thr[i], NULL);
printf("%u\n",thr_data[i].app);
}
return 0;
}
E questi sono i valori di pi greco calcolati con la nuova random:
| 3,141592109 | 3,141593705 | 3,141591164 | 3,141585824 | 3,141587683 |
Hanno una media di 3,141591584 e una deviazione standard di 0,000004660 e viene calcolato in circa 5 minuti dal mio computer. Probabilmente se tentassimo con più punti otterremmo un’approssimazione migliore, ma raggiungere la quinta cifra decimale per me vuol dire obiettivo raggiunto.
PS: dall’ultimo articolo sono cambiate un po’ di cose sul sito: sulla destra (se leggete da computer) o più in basso (se leggete da mobile) trovate un campo in cui potete inserire il vostro indirizzo mail per sapere quando viene pubblicato un nuovo articolo. In più in alto trovate la sezione contatti, se volete mettervi in contatto con me.
Bonus: se siete arrivati fino a qui a leggere meritate un bonus: due piccoli trucchetti in C che ho usato durante la stesura di questo articolo. Durante le computazioni, ripetute più volte e della durata anche di alcune decine di minuti, spesso mi allontanavo dal computer. Non potevo però fare a meno di controllare continuamente se il programma avesse restituito i risultati. Per evitare di controllare continuamente viene in aiuto la funzione Beep() di windows, che permette di emettere un suono della frequenza e durata desiderata in un certo punto del programma. Inserita alla fine del programma, il suono ci avviserà che è terminata la computazione.
#include <windows.h>
int main(int argc, char const *argv[]) {
/* codice */
Beep(3000, 500);
return 0;
}
Un altro piccolo escamotage che è utile conoscere è la funzione clock() che restituisce il numero di cicli di clock eseguiti dal processore dall’inizio del programma. Diventa utile per calcolare il tempo di esecuzione di un codice, utilizzata in combinazione con la costante CLOCKS_PER_SEC della libreria time.h, che contiene il numero di cicli di clock in ogni secondo. La funzione viene implementata come segue:
#include <time.h>
int main(int argc, char const *argv[]) {
clock_t begin = clock();
/* codice di cui misurare il tempo d'esecuzione */
clock_t end = clock();
printf("Tempo: %lf s\n", (double)(end - begin)/CLOCKS_PER_SEC);
return 0;
}
![]() This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Ottimo lavoro. Mi metterò a studiare il tuo codice!
Articolo molto interessante!
Interessante il sito ed anche i bonus 😉
Tienici aggiornati sul Forum Facebook di Arduino!
Il contenuto innanzi tutto !!! Questi sono articoli !
molto interessante
grazie
Caro Valerio complimenti … arriverai lontano o almeno te lo auguro.
Ciao
il prof. del Natta